Страницы: 1 2
Поиск| Автор | Сообщение |
|---|---|
|
Анатолий
#
10 ноя 2007 |
|
|
Максимович Игорь
#
12 ноя 2007 |
|
|
Анатолий
#
12 ноя 2007 |
|
|
Максимович Игорь
#
13 ноя 2007 |
|
|
Анатолий
#
13 ноя 2007 |
|
|
Анатолий
#
16 ноя 2007 |
|
|
Максимович Игорь
#
16 ноя 2007 |
Страницы: 1 2
Чтобы написать сообщение, необходимо войти или зарегистрироваться
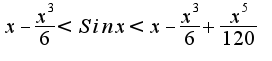
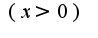 при фиксированном
при фиксированном 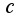 и достаточно больших
и достаточно больших 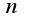 ,
, 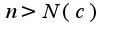 (биномиальный ряд!) имеем:
(биномиальный ряд!) имеем:
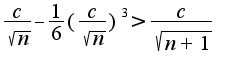 и соответсвенно:
и соответсвенно:
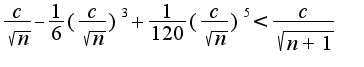 в зависимости от того, будет ли
в зависимости от того, будет ли 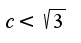 или
или 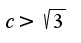 .
Пусть сначала
.
Пусть сначала 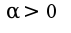 фиксировано и настолько большое, что
фиксировано и настолько большое, что 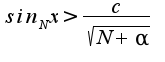 Тогда:
Тогда:
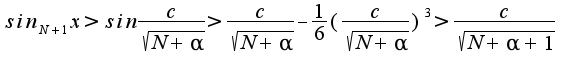 значит
значит 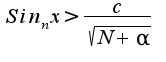 ,
, 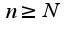 Отсюда
Отсюда 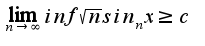 т.е.
т.е. 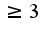 Когда
Когда 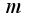 настолько большим, что
настолько большим, что 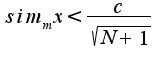 Тогда аналогично получаем, что:
Тогда аналогично получаем, что:
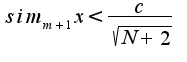
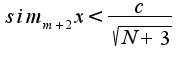 и т.д...
и т.д...