Поиск
| Автор | Сообщение |
|---|---|
|
trick
#
7 июн 2012 trick
7 июн 2012
|
|
|
o_a
#
7 июн 2012 |
|
|
trick
#
8 июн 2012 |
|
|
o_a
#
8 июн 2012 |
|
|
trick
#
8 июн 2012 |
|
|
o_a
#
8 июн 2012 |
|
|
trick
#
8 июн 2012 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
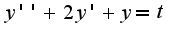 Находим изображение
Находим изображение
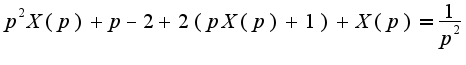 слева выносим X(p) за скобку и переносим вправо части без X(p)
слева выносим X(p) за скобку и переносим вправо части без X(p)
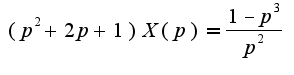
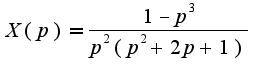 далее считаем методом неопределенных коэффициентов
далее считаем методом неопределенных коэффициентов
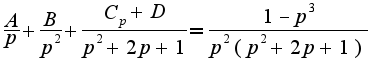
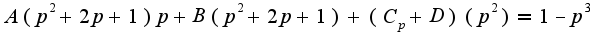
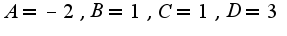 подставляем и получаем
подставляем и получаем
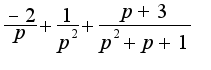 первые два слагаемых табличные, а вот с третьим проблема
первые два слагаемых табличные, а вот с третьим проблема
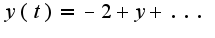 помогите перейти от изображения к соответствующем оригиналу, не удается преобразовать в табличный вид. Если все действия до этого были верными.
помогите перейти от изображения к соответствующем оригиналу, не удается преобразовать в табличный вид. Если все действия до этого были верными.
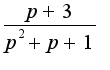
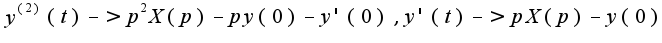 , поэтому надо знать начальные условия
, поэтому надо знать начальные условия 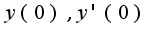 Откуда возникло уравнение
Откуда возникло уравнение 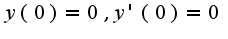
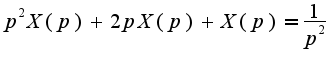 Сл-но,
Сл-но,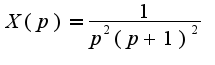 Разлагая это выражение на сумму дробей, получим
Разлагая это выражение на сумму дробей, получим 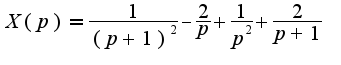 Возвращаясь по таблице изображений к переменной
Возвращаясь по таблице изображений к переменной 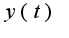 , получим
, получим