Страницы: 1 2
Поиск| Автор | Сообщение |
|---|---|
|
Ленка Фил
#
12 фев 2007 |
|
|
О.А.
#
12 фев 2007 |
|
|
Ленка Фил
#
12 фев 2007 |
|
|
О.А.
#
12 фев 2007 |
|
|
Ленка Фил
#
13 фев 2007 |
|
|
О.А.
#
13 фев 2007 |
|
|
О.А.
#
13 фев 2007 |
|
|
Ленка Фил
#
13 фев 2007 |
|
|
О.А.
#
13 фев 2007 |
|
|
Ленка Фил
#
13 фев 2007 |
|
|
О.А.
#
13 фев 2007 |
|
|
Ленка Фил
#
14 фев 2007 |
|
|
Ленка Фил
#
14 фев 2007 |
|
|
О.А.
#
14 фев 2007 |
|
|
Ленка Фил
#
14 фев 2007 |
Страницы: 1 2
Чтобы написать сообщение, необходимо войти или зарегистрироваться
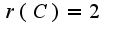 Так как ранг равен двум, то две переменные остаются произвольными, а две зависят от них, т.е.
Так как ранг равен двум, то две переменные остаются произвольными, а две зависят от них, т.е.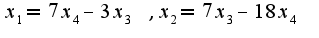 Подставляя значения
Подставляя значения 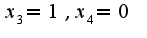 и
и 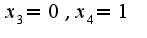 в
в 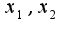 получим что общее решение однородной системы имеет вид:
получим что общее решение однородной системы имеет вид: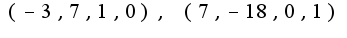 Тогда решение неоднородной системы :
Тогда решение неоднородной системы :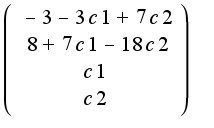
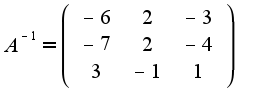 Кроме того, из определения обратнойи следует, что
Кроме того, из определения обратнойи следует, что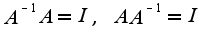 , где
, где 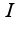 -единичная матрица
-единичная матрица