Поиск
| Автор | Сообщение |
|---|---|
|
Наталья
#
26 окт 2006 |
|
|
О.А.
#
26 окт 2006 |
|
|
наталья
#
26 окт 2006 |
|
|
О.А.
#
27 окт 2006 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
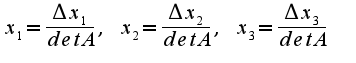 Где
Где 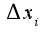 -определители матриц, полученные заменой первого и т.д.столбцов на столбец свободных членов.
-определители матриц, полученные заменой первого и т.д.столбцов на столбец свободных членов.![$A=|[1,-3,7],[3,-2,6],[2,1,-1]|$ $A=|[1,-3,7],[3,-2,6],[2,1,-1]|$](http://teacode.com/service/latex/latex.png?latex=A%3D%7C%5B1%2C-3%2C7%5D%2C%5B3%2C-2%2C6%5D%2C%5B2%2C1%2C-1%5D%7C&fontsize=21)
![$\Delta x_{1}=|[-2,-3,7],[-7,-2,6],[-5,1,-1]|$ $\Delta x_{1}=|[-2,-3,7],[-7,-2,6],[-5,1,-1]|$](http://teacode.com/service/latex/latex.png?latex=%5CDelta+x_%7B1%7D%3D%7C%5B-2%2C-3%2C7%5D%2C%5B-7%2C-2%2C6%5D%2C%5B-5%2C1%2C-1%5D%7C&fontsize=21) При условии, что
При условии, что