Поиск
| Автор | Сообщение |
|---|---|
|
О.А.
#
3 дек 2004 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
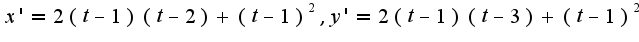 . Следовательно,
. Следовательно, 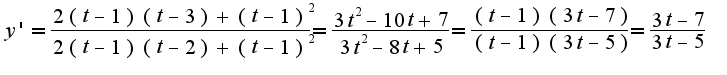 ,
8)
,
8) 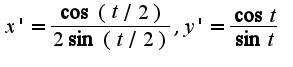 . След-но,
. След-но, 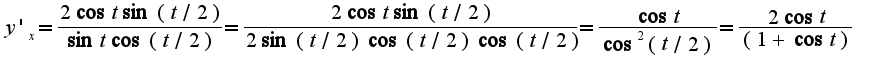 N13.197 1)
N13.197 1)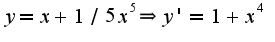 Сл-но,
Сл-но, 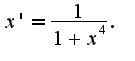 Так как
Так как 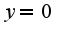 , то подставляем в исходную функцию вместо
, то подставляем в исходную функцию вместо 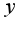 значение равное нулю, получим
значение равное нулю, получим 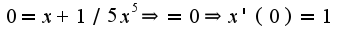 Аналогично, и для случая
Аналогично, и для случая 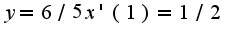 N13.207 7)
N13.207 7)