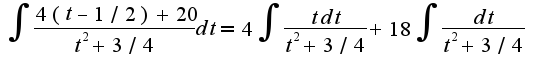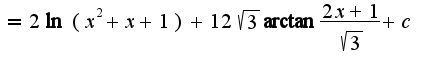Поиск
| Автор | Сообщение |
|---|---|
|
Оля
#
16 мар 2007 |
|
|
О.А.
#
16 мар 2007 |
|
|
Оля
#
17 мар 2007 |
|
|
О.А.
#
17 мар 2007 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
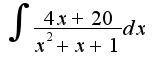
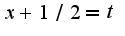 , в знаменателе надо выделить полный квадрат:
, в знаменателе надо выделить полный квадрат: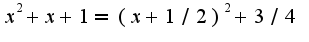
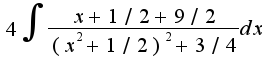 =
=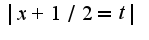
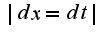 =
=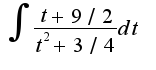 А что потом нужно делать? и какой ответ мы должны получить в конце?
А что потом нужно делать? и какой ответ мы должны получить в конце?