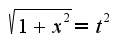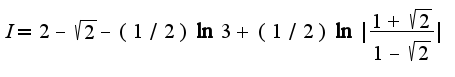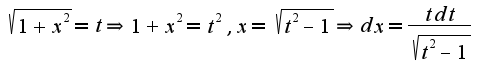Поиск
| Автор | Сообщение |
|---|---|
|
zaochnik
#
4 мая 2008 |
|
|
О.А.
#
4 мая 2008 |
|
|
zaochnik
#
6 мая 2008 |
|
|
zaochnik
#
6 мая 2008 |
|
|
zaochnik
#
16 мая 2008 |
|
|
zaochnik
#
19 мая 2008 |
|
|
О.А.
#
19 мая 2008 |
|
|
zaochnik
#
19 мая 2008 |
|
|
О.А.
#
19 мая 2008 |
|
|
zaochnik
#
19 мая 2008 |
|
|
О.А.
#
19 мая 2008 |
|
|
zaochnik
#
22 мая 2008 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
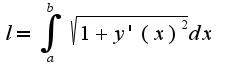 здесь
здесь 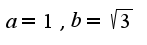 ,т.е.
,т.е.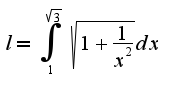 для того,чтобы вычислить данный интеграл,необходимо ввести замену
для того,чтобы вычислить данный интеграл,необходимо ввести замену