Поиск
Oleg Sh
#
20 дек 2006
|
Здравствуйте. Я по образованию гуманитарий. Сейчас пошел на второе высшее экономическое образование. Помогите пожалуйста исследовать функцию y=e^-x^2
Не могли бы Вы порекомендовать хороший справочник, где подробно разжеваны, с примерами, темы по математическому анализу?
Заранее спасибо!!!
|
О.А.
#
20 дек 2006
|
Есть учебник Красса М.С."Высшая математика для экономических специальностей"
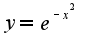 для нахождения горизонтальной асимптоты 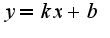 используем предел: 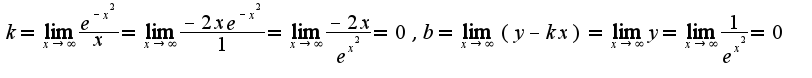 Таким образом уравнение асимптоты имеет вид 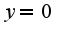
Кроме того область определения для функции вся числовая ось, область изменения- 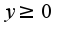 , функция является четной. Для нахождения экстремумов надо использовать первую производную 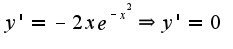 при 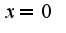 , т.к.первая производная меняет знак с плюса на минус при переходе через точку 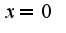 , то это точка максимума, по знаку второй производной находим интервалы выпуклости вверх и вниз. 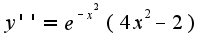 Точки перегиба: 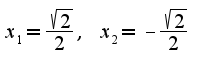 График имеет вид
http://matan.isu.ru/kons9.gif
|
Oleg Sh
#
20 дек 2006
|
Спасибо боьшое, Ольга Александровна, за столь скорый ответ. Был приятно удивлен такой оперативностью. Обязательно постараюсь купить рекомендованный Вами учебник. Еще раз выражаю слова благодарности.
|
Ваш ответ:
|
|
Чтобы написать сообщение, необходимо войти или зарегистрироваться
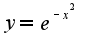 для нахождения горизонтальной асимптоты
для нахождения горизонтальной асимптоты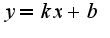 используем предел:
используем предел: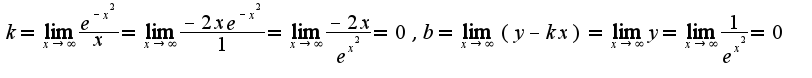 Таким образом уравнение асимптоты имеет вид
Таким образом уравнение асимптоты имеет вид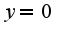 Кроме того область определения для функции вся числовая ось, область изменения-
Кроме того область определения для функции вся числовая ось, область изменения-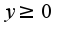 , функция является четной. Для нахождения экстремумов надо использовать первую производную
, функция является четной. Для нахождения экстремумов надо использовать первую производную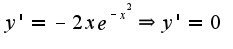 при
при 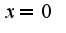 , т.к.первая производная меняет знак с плюса на минус при переходе через точку
, т.к.первая производная меняет знак с плюса на минус при переходе через точку 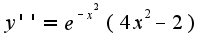 Точки перегиба:
Точки перегиба: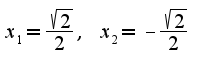 График имеет вид
http://matan.isu.ru/kons9.gif
График имеет вид
http://matan.isu.ru/kons9.gif