Поиск
| Автор | Сообщение |
|---|---|
|
ashtray_girl
#
7 апр 2006 |
|
|
О.А.
#
7 апр 2006 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
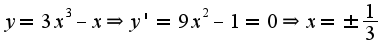 Исследование на экстремум происходит по знаку первой производной,т.е. при
Исследование на экстремум происходит по знаку первой производной,т.е. при 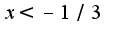 первая производная положительна, при
первая производная положительна, при 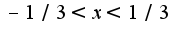 первая производная отрицательна, и при
первая производная отрицательна, и при 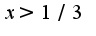 первая производная снова положительна, поэтому
первая производная снова положительна, поэтому 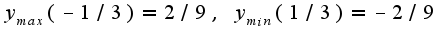
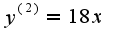 Отсюда ясно,что вторая производная меняет знак при переходе через ноль, поэтому точкаO(0,0)-точка перегиба, если
Отсюда ясно,что вторая производная меняет знак при переходе через ноль, поэтому точкаO(0,0)-точка перегиба, если 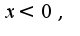 то график выпуклый вверх, а при
то график выпуклый вверх, а при 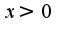 -выпуклый вниз.
-выпуклый вниз.