Поиск
| Автор | Сообщение |
|---|---|
|
Артур
#
22 апр 2020 |
|
|
o_a
#
22 апр 2020 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
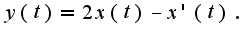 Найденную функцию подставим во второе уравнение системы, получим:
Найденную функцию подставим во второе уравнение системы, получим: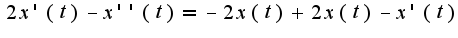 После упрощения получим,
После упрощения получим, 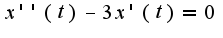 . Получено обычное однородное уравнение второго порядка с постоянными коэффициентами. Составим и решим характеристическое уравнение:
. Получено обычное однородное уравнение второго порядка с постоянными коэффициентами. Составим и решим характеристическое уравнение: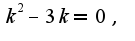 корни уравнения:
корни уравнения: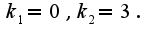 Сл-но, общее решение уравнения имеет вид:
Сл-но, общее решение уравнения имеет вид: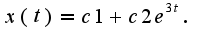 Находим вторую функцию:
Находим вторую функцию: 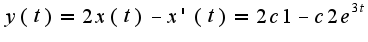 Чтобы найти частные решения системы, надо использовать начальные данные
Чтобы найти частные решения системы, надо использовать начальные данные 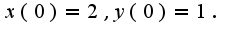 Таким образом,
Таким образом, 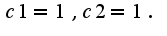 Окончательный вид частного решения системы
Окончательный вид частного решения системы