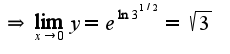Поиск
| Автор | Сообщение |
|---|---|
|
Константин
#
19 дек 2007 |
|
|
О.А.
#
19 дек 2007 |
|
|
Константин
#
19 дек 2007 |
|
|
О.А.
#
19 дек 2007 |
|
|
Константин
#
20 дек 2007 |
|
|
Константин
#
20 дек 2007 |
|
|
О.А.
#
20 дек 2007 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
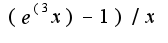 в степени
в степени 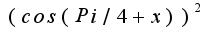 Пожалуйста помогите.Заранее спасибо!!!
Пожалуйста помогите.Заранее спасибо!!!
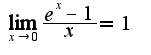 , поэтому предел основания равен 3, предел показателя 1/2, сл-но, предел равен
, поэтому предел основания равен 3, предел показателя 1/2, сл-но, предел равен 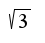
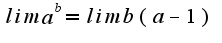 ответ sqrt(3), а решение неправильное.
Пожалуйста подскажите. Заранее спасибо!!!
ответ sqrt(3), а решение неправильное.
Пожалуйста подскажите. Заранее спасибо!!!
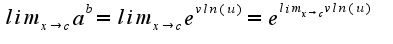 вот эта формула правильная а ответ получается не
вот эта формула правильная а ответ получается не