Поиск
| Автор | Сообщение |
|---|---|
|
Катя
#
3 мар 2008 |
|
|
О.А.
#
3 мар 2008 |
|
|
Катя
#
4 мар 2008 |
|
|
О.А.
#
4 мар 2008 |
|
|
Катя
#
4 мар 2008 |
|
|
О.А.
#
4 мар 2008 |
|
|
Катя
#
4 мар 2008 |
|
|
О.А.
#
4 мар 2008 |
|
|
Катя
#
4 мар 2008 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
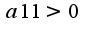 -то точка минимума,если
-то точка минимума,если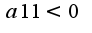 , то максимум. Градиент-это вектор, имеющий координаты
, то максимум. Градиент-это вектор, имеющий координаты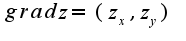
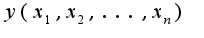 по одной ,например,
по одной ,например,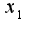 надо предположить, что остальные являются фиксированными числами.Например,
надо предположить, что остальные являются фиксированными числами.Например,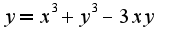 Находим производную по
Находим производную по  ,считаем
,считаем 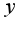 фиксированным числом,поэтому
фиксированным числом,поэтому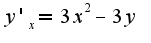 , аналогично,
, аналогично,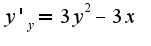
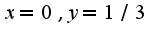 экстремума нет,т.к. определитель матрицы отрицательный, а при
экстремума нет,т.к. определитель матрицы отрицательный, а при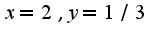 -минимум,т.к.
-минимум,т.к. 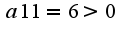 , чтобы найти градиент в некоторой точке, надо найти частные производные первого порядка и посчитать их в указанной точке, об этом я уже писала
, чтобы найти градиент в некоторой точке, надо найти частные производные первого порядка и посчитать их в указанной точке, об этом я уже писала