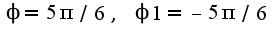Поиск
| Автор | Сообщение |
|---|---|
|
Константин
#
2 мар 2008 |
|
|
Сергей
#
17 мар 2008 |
|
|
О.А.
#
17 мар 2008 |
|
|
Сергей
#
18 мар 2008 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
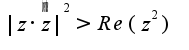 где
где 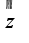 -сопряж. Z
-сопряж. Z
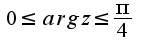
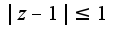 Границы области, ей принадлежащие, вычертить сплошными, а непринадлежащие-пунктирными линиями.
Я принял
Границы области, ей принадлежащие, вычертить сплошными, а непринадлежащие-пунктирными линиями.
Я принял 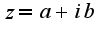 получилось, что
получилось, что 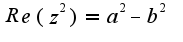 а
а 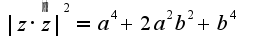 Относительно второго неравенства получается, что угол
Относительно второго неравенства получается, что угол 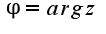
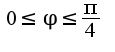 Что касается третьего неравенства, то у меня получилось, что
Что касается третьего неравенства, то у меня получилось, что
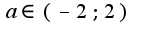 и
и 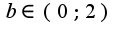 Но пожоже, что это не правильно, так как построить область не получается. Пожалуйста помогите!!! Заранее спасибо!!!
Но пожоже, что это не правильно, так как построить область не получается. Пожалуйста помогите!!! Заранее спасибо!!!
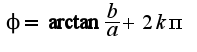 При определении значения аргумента надо ориентироваться на графическое изображение комплексного числа
При определении значения аргумента надо ориентироваться на графическое изображение комплексного числа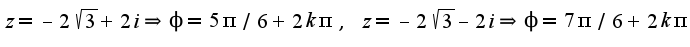 Главным значением обычно называют наименьшее по абсолютной величине значение, поэтому главными значениями аргумента будут
Главным значением обычно называют наименьшее по абсолютной величине значение, поэтому главными значениями аргумента будут