Поиск
| Автор | Сообщение |
|---|---|
|
Silov
#
15 дек 2008 |
|
|
О.А.
#
21 мая 2005 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
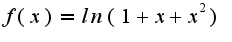 ,
, 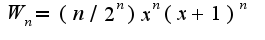
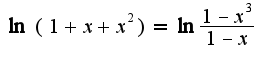 .Далее используем свойство логарифмов:
.Далее используем свойство логарифмов: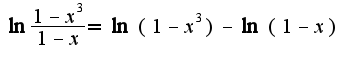 Далее используя известное разложение в ряд по степеням x
для логарифма, получим:
Далее используя известное разложение в ряд по степеням x
для логарифма, получим: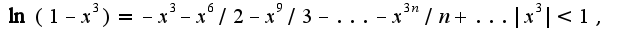
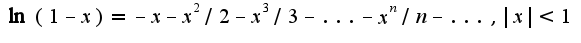 Поэтому
Поэтому 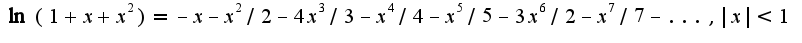 Что касается второй функции нужно уточнить по каким степеням нужно произвести разложение, т.к. она является полиномом степени 2n и фактически уже имеет представление как по степеням x, так и по степеням x+1
Что касается второй функции нужно уточнить по каким степеням нужно произвести разложение, т.к. она является полиномом степени 2n и фактически уже имеет представление как по степеням x, так и по степеням x+1