Поиск
| Автор | Сообщение |
|---|---|
|
Оля
#
23 дек 2006 |
|
|
Оля
#
23 дек 2006 |
|
|
Оля
#
23 дек 2006 |
|
|
О.А.
#
23 дек 2006 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
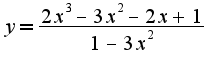 Затем нужно было найти асимптоты, я их нашла,
а)вертикальные
Затем нужно было найти асимптоты, я их нашла,
а)вертикальные
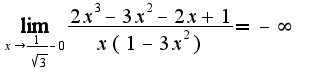
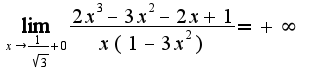
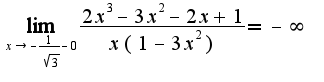
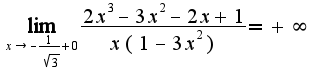 Получается что
Получается что 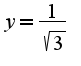 и
и 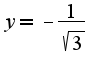 - вертикальные асимптоты
б)наклонные
- вертикальные асимптоты
б)наклонные
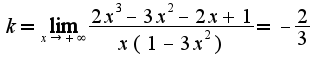
![$b=\lim_{x\rightarrow+\infty}[\frac{2x^3-3x^2-2x+1}{1-3x^2}+\frac{2x}{3}]=-\frac{2}{3}$ $b=\lim_{x\rightarrow+\infty}[\frac{2x^3-3x^2-2x+1}{1-3x^2}+\frac{2x}{3}]=-\frac{2}{3}$](http://teacode.com/service/latex/latex.png?latex=b%3D%5Clim_%7Bx%5Crightarrow%2B%5Cinfty%7D%5B%5Cfrac%7B2x%5E3-3x%5E2-2x%2B1%7D%7B1-3x%5E2%7D%2B%5Cfrac%7B2x%7D%7B3%7D%5D%3D-%5Cfrac%7B2%7D%7B3%7D&fontsize=21) Получается наклонная асимптота - это
Получается наклонная асимптота - это 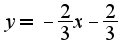 Проверьте пожалуйста
Проверьте пожалуйста
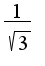 и
и 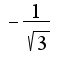 разрыва второго рода, поскольку два односторониих предела равны бесконечности? Как в данном случае оформить в задании на иследование вышезаданной функции в пункте Непрерывность?
разрыва второго рода, поскольку два односторониих предела равны бесконечности? Как в данном случае оформить в задании на иследование вышезаданной функции в пункте Непрерывность?
 Вертикальная асимптота
Вертикальная асимптота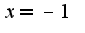 , а наклонная или горизонтальная - это ось ОХ?
, а наклонная или горизонтальная - это ось ОХ?
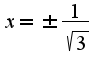 , а у вас написанро в знаменателе дроби лишнее x. Кроме того, неправильно нашли значение b, предел равен единице. В точках
, а у вас написанро в знаменателе дроби лишнее x. Кроме того, неправильно нашли значение b, предел равен единице. В точках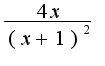 .
. 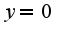 -горизонтальная ,
-горизонтальная ,