Страницы: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
Поиск| Автор | Сообщение |
|---|---|
|
Элли
#
3 дек 2012 |
|
|
o_a
#
3 дек 2012 |
|
|
Элли
#
3 дек 2012 |
|
|
o_a
#
3 дек 2012 |
|
|
Элли
#
5 дек 2012 |
|
|
Ксения
#
5 дек 2012 |
|
|
o_a
#
5 дек 2012 |
|
|
Даша
#
10 дек 2012 |
|
|
Ксения
#
17 дек 2012 Ксения
17 дек 2012
|
|
|
o_a
#
17 дек 2012 |
|
|
Ксения
#
17 дек 2012 |
|
|
Малис
#
18 дек 2012 |
|
|
o_a
#
18 дек 2012 |
|
|
Alexx
#
21 дек 2012 |
|
|
o_a
#
21 дек 2012 |
Страницы: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
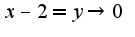 , затем использовать следствие из первого замечательного предела
, затем использовать следствие из первого замечательного предела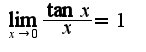
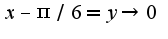 Дальше проделать преобразования, учитывая формулы тригонометрии, ответ 1
2)
Дальше проделать преобразования, учитывая формулы тригонометрии, ответ 1
2)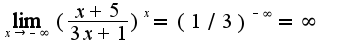 3) непосредственно подставить в функцию предельную точку
3) непосредственно подставить в функцию предельную точку 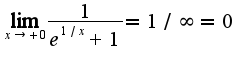
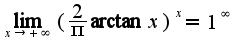 Полагаем
Полагаем 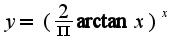 Сл-но,
Сл-но, 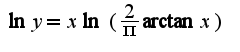 Находим предел от логарифма
Находим предел от логарифма 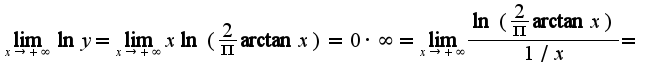
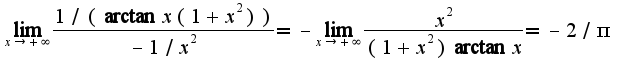 Таким образом, имеем
Таким образом, имеем 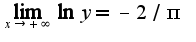 Сл-но,
Сл-но, 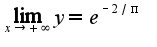 17.58Нужно использовать правило Лопиталя дважды
17.58Нужно использовать правило Лопиталя дважды
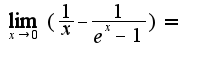
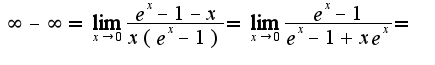
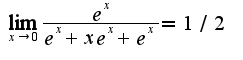 Для решения номера 17.50 нужно преобразовать выражение, оставив в числителе более сложный сомножитель, в знаменатель-
Для решения номера 17.50 нужно преобразовать выражение, оставив в числителе более сложный сомножитель, в знаменатель- 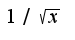
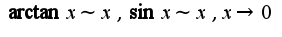
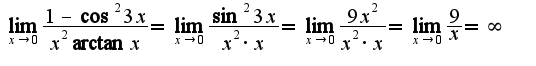
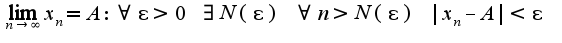 Для данного примера получим:
Для данного примера получим: 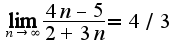
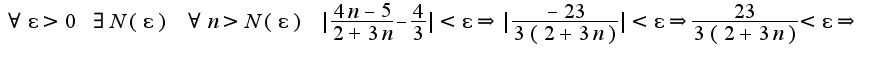
![$\frac{3(2+3n)}{23}>\frac{1}{\epsilon}\Rightarrow 2+3n>\frac{23}{3\epsilon}\Rightarrow n>\frac{23}{9\epsilon}-\frac{2}{3}\Rightarrow N(\epsilon)=[\frac{23}{9\epsilon}-\frac{2}{3}]$ $\frac{3(2+3n)}{23}>\frac{1}{\epsilon}\Rightarrow 2+3n>\frac{23}{3\epsilon}\Rightarrow n>\frac{23}{9\epsilon}-\frac{2}{3}\Rightarrow N(\epsilon)=[\frac{23}{9\epsilon}-\frac{2}{3}]$](http://teacode.com/service/latex/latex.png?latex=%5Cfrac%7B3%282%2B3n%29%7D%7B23%7D%3E%5Cfrac%7B1%7D%7B%5Cepsilon%7D%5CRightarrow+2%2B3n%3E%5Cfrac%7B23%7D%7B3%5Cepsilon%7D%5CRightarrow+n%3E%5Cfrac%7B23%7D%7B9%5Cepsilon%7D-%5Cfrac%7B2%7D%7B3%7D%5CRightarrow+N%28%5Cepsilon%29%3D%5B%5Cfrac%7B23%7D%7B9%5Cepsilon%7D-%5Cfrac%7B2%7D%7B3%7D%5D&fontsize=21)