Поиск
| Автор | Сообщение |
|---|---|
|
Алекс
#
29 мар 2007 |
|
|
О.А.
#
29 мар 2007 |
|
|
Алекс
#
29 мар 2007 |
|
|
Алекс
#
29 мар 2007 |
|
|
О.А.
#
29 мар 2007 |
|
|
Student
#
16 дек 2009 |
|
|
О.А.
#
16 дек 2009 |
|
|
Student
#
16 дек 2009 |
|
|
О.А.
#
16 дек 2009 |
|
|
Катя
#
23 дек 2009 |
|
|
О.А.
#
23 дек 2009 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
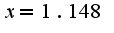 Наклонных асимптот нет,вертикальных две в силу области определения
Наклонных асимптот нет,вертикальных две в силу области определения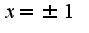
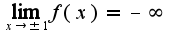 Рекомендую использовать пакет Maple для построения графиков
Рекомендую использовать пакет Maple для построения графиков