Страницы: 1 2
Поиск| Автор | Сообщение |
|---|---|
|
Евгений.math
#
20 окт 2008 |
|
|
О.А.
#
20 окт 2008 |
|
|
новичок
#
20 окт 2008 |
|
|
О.А.
#
20 окт 2008 |
|
|
Евгений.math
#
21 окт 2008 |
|
|
Алекс
#
10 янв 2009 |
|
|
Алекс
#
10 янв 2009 |
|
|
О.А.
#
10 янв 2009 |
|
|
КРИСТИНОЧКА
#
14 июн 2009 |
|
|
О.А.
#
14 июн 2009 |
|
|
КРИСТИНОЧКА
#
14 июн 2009 |
|
|
Саша
#
14 июн 2009 |
|
|
Саша
#
14 июн 2009 |
|
|
Д.
#
18 июн 2009 |
|
|
О.А.
#
18 июн 2009 |
Страницы: 1 2
Чтобы написать сообщение, необходимо войти или зарегистрироваться
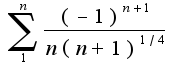 данный ряд это ряд Лейбница,т.к. выполнены два условия признака Лейбница
1)члены ряда по модулю образуют монотонно убывающую последовательность
данный ряд это ряд Лейбница,т.к. выполнены два условия признака Лейбница
1)члены ряда по модулю образуют монотонно убывающую последовательность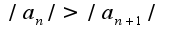 2)
2)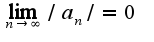 , поэтому данный ряд сходится, если составить ряд из модулей членов ряда, то ряд
, поэтому данный ряд сходится, если составить ряд из модулей членов ряда, то ряд 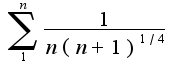 сходится как обобщенный гармонический с показателем
сходится как обобщенный гармонический с показателем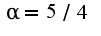 , поэтому исходный ряд сх-ся абсолютно
, поэтому исходный ряд сх-ся абсолютно
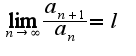 если
если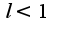 , то ряд сходится, если
, то ряд сходится, если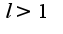 , то ряд расходится
, то ряд расходится
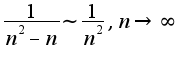 а ряд
а ряд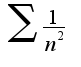 сходится, то исходный ряд сходится абсолютно
сходится, то исходный ряд сходится абсолютно