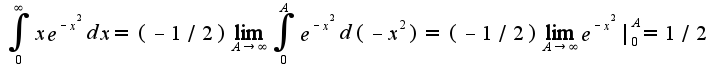Поиск
| Автор | Сообщение |
|---|---|
|
Эллина
#
2 ноя 2009 |
|
|
О.А.
#
2 ноя 2009 |
|
|
Эллина
#
3 ноя 2009 |
|
|
Эллина
#
3 ноя 2009 |
|
|
О.А.
#
3 ноя 2009 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
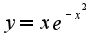
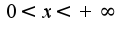 Какой алгоритм решения?
Какой алгоритм решения?
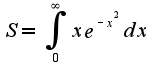
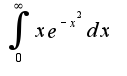 ;
;
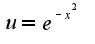
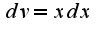
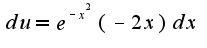
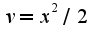
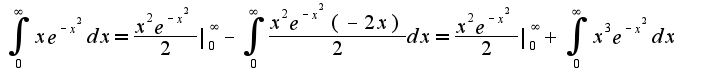 не... я только усложнила... По какому принципу (формуле) считать?
не... я только усложнила... По какому принципу (формуле) считать?
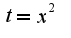
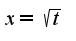
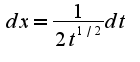
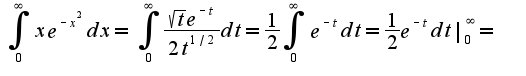 Или так?
Или так?