Поиск
| Автор | Сообщение |
|---|---|
|
Света
#
16 янв 2008 |
|
|
О.А.
#
16 янв 2008 |
|
|
Света
#
16 янв 2008 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
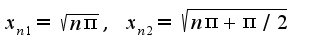 и использовать отрицание определения равномерной непрерывности, как я уже объяснила для другой функции
и использовать отрицание определения равномерной непрерывности, как я уже объяснила для другой функции