дифференциальное уравнение

Автор	Сообщение
Оксана # 14 дек 2007	Не знаю как решать(((( y` - y/ x+3 = e^2x (x+3)
Владимир # 14 дек 2007	Это линейное дифф. уравнение. Есть несколько способов решения. Например, можно решить с помощью замены $y=u(x)v(x)$ , $y' = u'v + uv'$ Получается: $u'v+uv' -\frac{uv}{x+3} = e^{2x}(x+3);$ $u'v+u(v' -\frac{v}{x+3}) = e^{2x}(x+3);$ $v' -\frac{v}{x+3} = 0 => \frac{dv}{dx} = \frac{v}{x+3} => \int \frac{dv}{v} = \int\frac{dx}{x+3} => \ln{\|v\|} = \ln{\|x+3\|};$ $v = x+3;$ $u'v = e^{2x}(x+3) => u'(x+3) = e^{2x}(x+3) => \frac{du}{dx} = e^{2x} => \int du = \int e^{2x}dx + C;$ $u = \frac{e^{2x}}{2} + C$ Ответ: $y = (\frac{e^{2x}}{2} + C)(x+3)$ Вроде нигде не ошибся :)
Оксана # 14 дек 2007	СПАСИБО Вам ООООООООООООООГРОМНОЕ!!!!!!!
Ваш ответ:	Чтобы написать сообщение, необходимо войти или зарегистрироваться

Оксана #
14 дек 2007

Не знаю как решать(((( y` - y/ x+3 = e^2x (x+3)

Владимир #
14 дек 2007

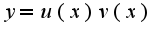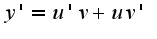Это линейное дифф. уравнение. Есть несколько способов решения. Например, можно решить с помощью замены $y=u(x)v(x)$ , $y' = u'v + uv'$ Получается: 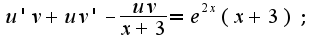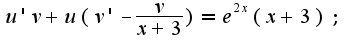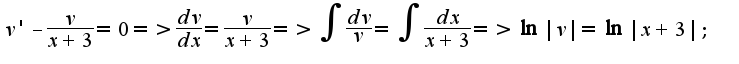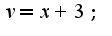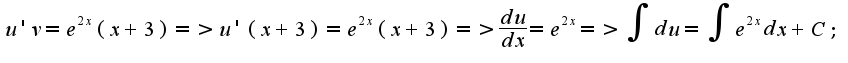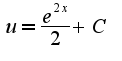$u'v+uv' -\frac{uv}{x+3} = e^{2x}(x+3);$ $u'v+u(v' -\frac{v}{x+3}) = e^{2x}(x+3);$ $v' -\frac{v}{x+3} = 0 => \frac{dv}{dx} = \frac{v}{x+3} => \int \frac{dv}{v} = \int\frac{dx}{x+3} => \ln{|v|} = \ln{|x+3|};$ $v = x+3;$ $u'v = e^{2x}(x+3) => u'(x+3) = e^{2x}(x+3) => \frac{du}{dx} = e^{2x} => \int du = \int e^{2x}dx + C;$ $u = \frac{e^{2x}}{2} + C$ Ответ: 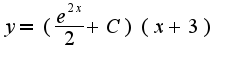$y = (\frac{e^{2x}}{2} + C)(x+3)$ Вроде нигде не ошибся :)

Оксана #
14 дек 2007

СПАСИБО Вам ООООООООООООООГРОМНОЕ!!!!!!!

Ваш ответ:

Teacode.com: дифференциальное уравнение