Страницы: 1 2
Поиск| Автор | Сообщение |
|---|---|
|
О.А.
#
12 мар 2008 |
|
|
Виктор
#
12 мар 2008 |
|
|
Виктор
#
12 мар 2008 |
|
|
О.А.
#
12 мар 2008 |
|
|
Виктор
#
13 мар 2008 |
|
|
Виктор
#
14 мар 2008 |
|
|
О.А.
#
14 мар 2008 |
|
|
Виктор
#
21 мар 2008 |
Страницы: 1 2
Чтобы написать сообщение, необходимо войти или зарегистрироваться
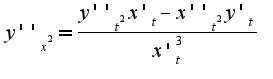 , предварительно надо найти первые производные
, предварительно надо найти первые производные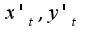 , затем вторые и подставить в данную формулу
, затем вторые и подставить в данную формулу
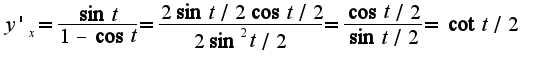
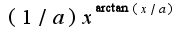 , то надо вынести константу
, то надо вынести константу 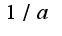 за знак производной и логарифмировать, потом находить производную
за знак производной и логарифмировать, потом находить производную