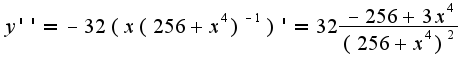Поиск
| Автор | Сообщение |
|---|---|
|
Алексей
#
16 апр 2012 |
|
|
o_a
#
16 апр 2012 |
|
|
Алексей
#
16 апр 2012 |
|
|
o_a
#
16 апр 2012 |
|
|
Алексей
#
16 апр 2012 |
|
|
paulinio
#
20 мая 2012 |
|
|
o_a
#
21 мая 2012 |
|
|
Елена
#
26 мар 2013 Елена
1 апр 2013
|
|
|
o_a
#
1 апр 2013 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
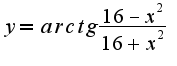 Помогите найти первую и вторую производную.
Пытался дифференцировать "в лоб" как сложную функцию, но получается как то через чур всё запутанно.
Заранее спасибо.
Помогите найти первую и вторую производную.
Пытался дифференцировать "в лоб" как сложную функцию, но получается как то через чур всё запутанно.
Заранее спасибо.
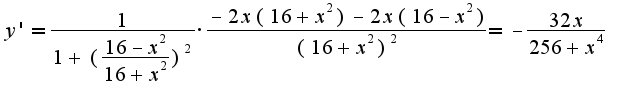 Вторая производная находится аналогично, как производная от произведения
Вторая производная находится аналогично, как производная от произведения