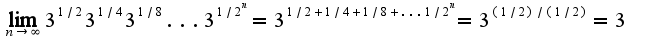Поиск
Оксана
#
31 мая 2006
|
Пожалуйста помогите! Мне уже много лет, я получаю высшее для работы. Высшую математику я уже не помню. Мне нужно решить задания по трем темам с несколькими примерами. Прошу, помогите! И простите за то, что буду писать "по турецки". Вот первая тема:
1) lim (X стремится к 0) tg2X
_____
sin5X
2) lim (X стремится к 0) tgX - sinX
__________
3
X
3) lim (X стремится к 0) корень из 4+X - 2
_________________
X
4)lim (X стремится к 0) 3X
_____________________________
корень из X+3 - корень из 3-X
П П
5) lim (X стремится к 0) sin(X + _) + sin(- _)
3 3
______________________
2X
6) lim (X стремится к 0) X(tgX + ctgX)
_____________
2
2
7)lim (X стремится к бесконечности) X(корень из X+1 - X)
8)lim (X стремится к бесконечности) X(ln(X+1) - lnX)
3
9)lim (X стремится к бесконечности) общая скобка 5X + 2
_____
3
5X
общая скобка закрывается и все в корне из X
10) lim (n стремится к бесконечности) корень из 3 * корень из 3 (на галке корня стоит цифра 4) * корень из 3 (на галке корня стоит цифра 8)....корень из 3(на галке корня стоит 2n)
Я еще напишу Вам чуть позже 2 задания. хотелось бы сначала узнать решение по этим примерам первого задания.
С уважением,
Оксана
|
О.А.
#
31 мая 2006
|
Условия некоторых примеров трудно понять, плэтому пишу решения тех, которые удалось расшифровать:
1) 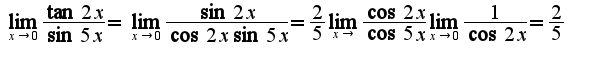
2) 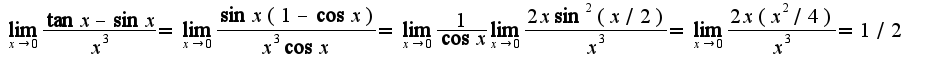
3) 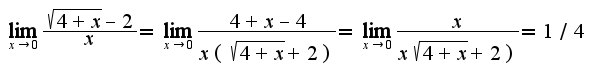
4) 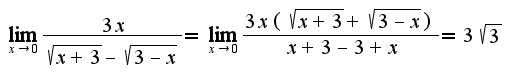
7) 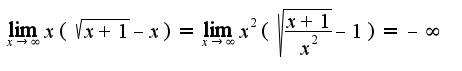
10) 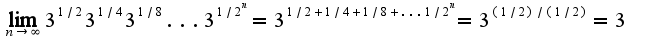
|
Ваш ответ:
|
|
Чтобы написать сообщение, необходимо войти или зарегистрироваться
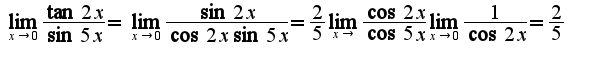 2)
2)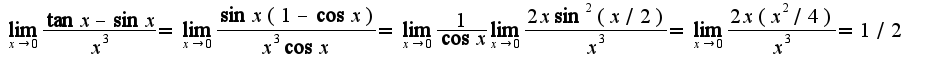 3)
3)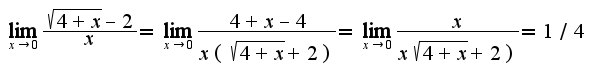 4)
4)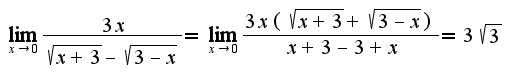 7)
7)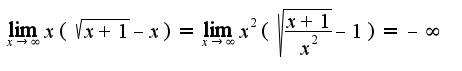 10)
10)