Поиск
| Автор | Сообщение |
|---|---|
|
Станислав Матвеев
#
вчера в 18:03 |
|
|
О.А.
#
10 ноя 2004 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
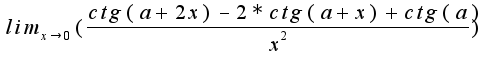 2)
2)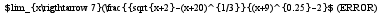
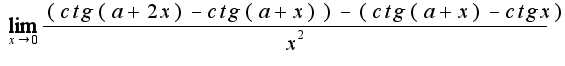 . Затем используем формулу для разности котангенсов для каждой круглой скобки:
. Затем используем формулу для разности котангенсов для каждой круглой скобки: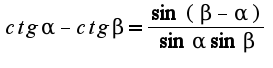
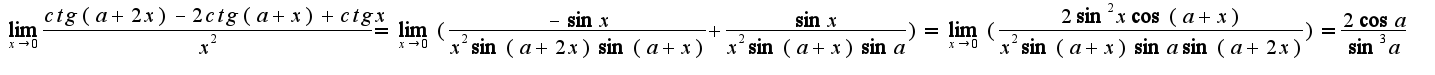 2)
2)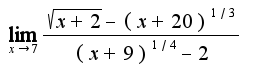 Для нахождения предела используем замену эквивалентных величин:
Для нахождения предела используем замену эквивалентных величин:
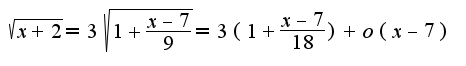
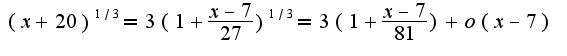
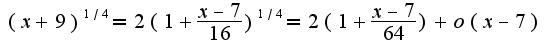 Подставляя в предел, получим,
Подставляя в предел, получим,