Поиск
| Автор | Сообщение |
|---|---|
|
Виктор
#
4 апр 2007 |
|
|
О.А.
#
4 апр 2007 |
|
|
Виктор
#
4 апр 2007 |
|
|
Виктор
#
4 апр 2007 |
|
|
О.А.
#
4 апр 2007 |
|
|
Виктор
#
4 апр 2007 |
|
|
О.А.
#
4 апр 2007 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
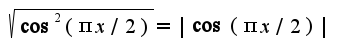 Во-вторых, неправильно подставляете пределы в первообразную,т.к.
Во-вторых, неправильно подставляете пределы в первообразную,т.к.