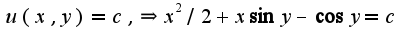Поиск
| Автор | Сообщение |
|---|---|
|
Robert
#
28 сен 2007 |
|
|
О.А.
#
28 сен 2007 |
|
|
Robert
#
5 окт 2007 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
 Метод решения следующий:
нужно найти функцию
Метод решения следующий:
нужно найти функцию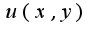 , для которой левая часть является полным дифференциалом.Из данного уравнения следует, что
, для которой левая часть является полным дифференциалом.Из данного уравнения следует, что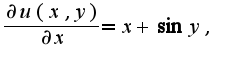 поэтому интегрируя данное выражение, получим
поэтому интегрируя данное выражение, получим 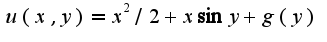 Найдем
Найдем 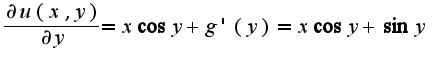 Сл-но,
Сл-но, 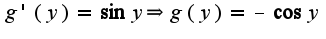 Таким образом,
Таким образом, 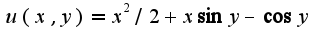 Общим интегралом данного уравнения будет
Общим интегралом данного уравнения будет