Поиск
| Автор | Сообщение |
|---|---|
|
Константин
#
13 апр 2008 |
|
|
О.А.
#
13 апр 2008 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
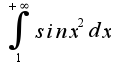 б)
б) 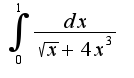 Пожалуйста помогите!!! Заранее спасибо!!!
Пожалуйста помогите!!! Заранее спасибо!!!
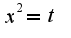 , затем применить признак Абеля-Дирихле,данный интеграл сходится
2)особая точка подинтегральной функции-это нуль,поэтому ищем эквивалентную функцию в нуле
, затем применить признак Абеля-Дирихле,данный интеграл сходится
2)особая точка подинтегральной функции-это нуль,поэтому ищем эквивалентную функцию в нуле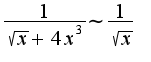 при
при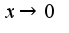 поскольку
поскольку 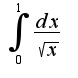 -сходится,т.к.
-сходится,т.к.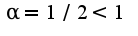 , то исходный тоже сходится
, то исходный тоже сходится