Alan
#
4 мая 2009
|
Здравствуйте.
Прошу помощи, чтобы разобраться в переходе к полярным координатам, и цилиндрическим. Преподаватель оставил эту тему, если это можно так сказать, на личное изучение. Сколько не ищу материалов, не могу никак разобраться. Нужно на простом примере разобрать это.
Вот, например, дано задание.
S - "знак интеграла"
p - "ро"
ф - угол "фи"
п - "пи"
Перейти в двойном интеграле
SSf(x,y)dxdy к полярным координатам, и расставить пределы интегрирования, где D-круг,
1). x^2 + y^2 (меньше или равно) R^2
2). x^2 + y^2 (меньше или равно) ax
И так, начинаем с того, что пишем координаты определяющие уравнения в полярной системе координат:
{x = p sin ф
{y = p sin ф
{(0,0) <=> (0,0)
теперь просто подставляем:
1) первый случай
_____________x^2 + y^2 (меньше или равно) R^2
р^2 cos ф^2 + р^2 sin ф^2 (меньше или равно) R^2
___________________р^2 (меньше или равно) R^2
_____________________р (меньше или равно) R
И вот здесь главный момент. Что теперь мне это даёт. Как нарисовать это в полярной системе и самое важное, как найти пределы интегрирования, т.е как изменяется "р" и "ф" ?
Ответ у меня есть, он в данном случае не самое главное:
2п____R_____________________________- пределы интегрирования
Sdф___S f(p cos ф, р sin ф)рdр
0_____0_____________________________- пределы интегрирования
2) И для второго случая:
_____________x^2 + y^2 (меньше или равно) ax
р^2 cos ф^2 + р^2 sin ф^2 (меньше или равно) aр cos ф
___________________р^2 (меньше или равно) aр cos ф
____________________р (меньше или равно) a cos ф
И ответ.
п/2____acosф_____________________
Sdф___ S f(p cos ф, р sin ф)рdр
-п/2___0___________________________
(Из всего этого, можно сделать вывод, что "р" изменяется ВСЕГДА от нуля до чего-то, в зависмости от заданной функции. А вот с правильным нахождением "ф" мне никак не понять, как это связать с заданным уравнением)
Вот пока всё. Если поможете разобраться, как просто искать пределы интегрирования и как это зарисовать, спрошу уже про цилиндрические координаты.
Надеюсь на вашу помощь.
|
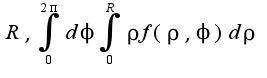 2) тоже окружность, уравнение которой в декартовой системе
2) тоже окружность, уравнение которой в декартовой системе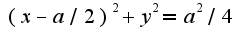 , подставляя замену в уравнение окружности, получим
, подставляя замену в уравнение окружности, получим