Поиск
| Автор | Сообщение |
|---|---|
|
Maksim Конанов
#
14 окт 2005 |
|
|
О.А.
#
14 окт 2005 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
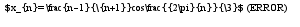 (Извените в Latex-е почемуто не получилось) Находить подпоследовательноси и частичные пределы.Зарание спасибо.
(Извените в Latex-е почемуто не получилось) Находить подпоследовательноси и частичные пределы.Зарание спасибо.
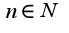 можно убедиться(можно взять значения
можно убедиться(можно взять значения 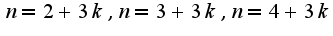 ), что все элементы данной последовательности содержатся в двух подпоследовательностях:
), что все элементы данной последовательности содержатся в двух подпоследовательностях: 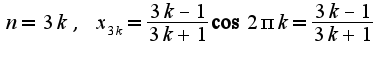 и
и 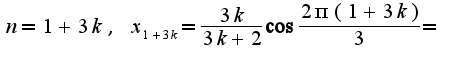
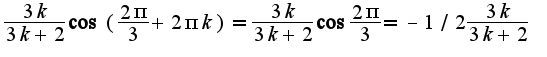 И находя пределы указанных последовательностей, получим
И находя пределы указанных последовательностей, получим 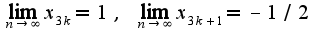 Кроме того, нижний предел последовательности равен наименьшему частичному пределу, а верхний предел равен наибольшему частичному пределу.Поэтому нижний предел для данной последовательности равен -1/2, а верхний - 1.
Кроме того, нижний предел последовательности равен наименьшему частичному пределу, а верхний предел равен наибольшему частичному пределу.Поэтому нижний предел для данной последовательности равен -1/2, а верхний - 1.