Поиск
| Автор | Сообщение |
|---|---|
|
Лиза
#
30 окт 2008 |
|
|
Иван Иванов
#
30 окт 2008 |
|
|
Лиза
#
30 окт 2008 |
|
|
Лиза
#
30 окт 2008 |
|
|
О.А.
#
30 окт 2008 |
|
|
Лиза
#
31 окт 2008 |
|
|
О.А.
#
31 окт 2008 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
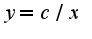 , затем, считая,что константа
, затем, считая,что константа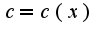 ,зависит от
,зависит от (метод называется вариацией произвольной константы), подставим в исходное уравнение:
(метод называется вариацией произвольной константы), подставим в исходное уравнение: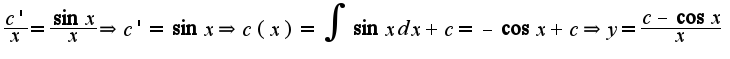
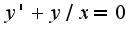 ,решение данного уравнения:
,решение данного уравнения: