Поиск
| Автор | Сообщение |
|---|---|
|
SpY
#
22 янв 2006 |
|
|
О.А.
#
22 янв 2006 |
|
|
SpY
#
23 янв 2006 |
|
|
SpY
#
23 янв 2006 |
|
|
SpY
#
23 янв 2006 |
|
|
О.А.
#
24 янв 2006 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
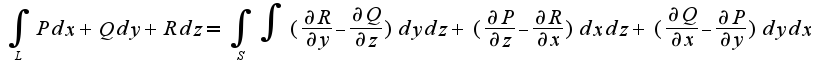 В данной задаче
В данной задаче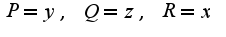 Поэтому
Поэтому 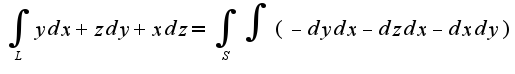 Учитывая, что в сечении шара плоскостью
Учитывая, что в сечении шара плоскостью 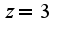 получается окружность:
получается окружность: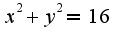 получим, что циркуляция равна:
получим, что циркуляция равна: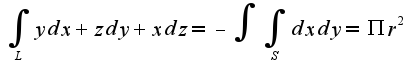 , где
, где 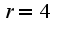 -радиус окружности, полученной в сечении шара плоскостью
-радиус окружности, полученной в сечении шара плоскостью 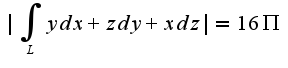 Непосредственное вычисление:
Непосредственное вычисление: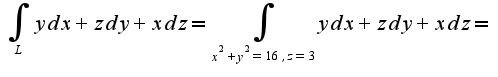
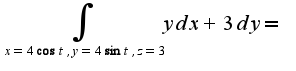
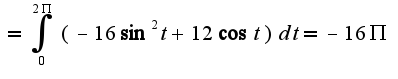
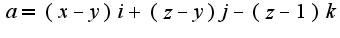 Г=
Г=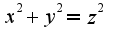
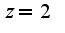 2)
2)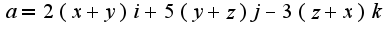 Г=
Г=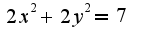
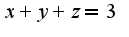
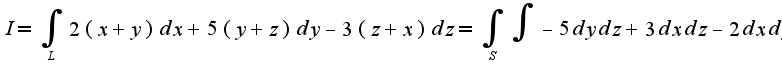
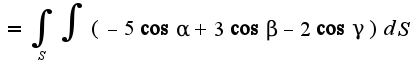 ,где S-множество
,где S-множество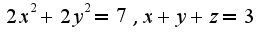 Множество S проектируется на плоскость XOYв круг
Множество S проектируется на плоскость XOYв круг 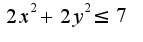 . Переходя от поверхностного интеграла к двойному и учитывая, что
. Переходя от поверхностного интеграла к двойному и учитывая, что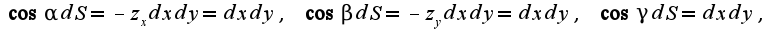 получим
получим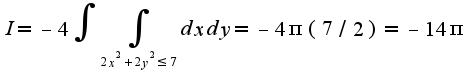 .
.