| Автор | Сообщение |
|---|---|
|
О.А.
#
2 мая 2009 |
|
|
Яся
#
2 мая 2009 |
|
|
ABTOPuTET
#
15 мая 2009 |
|
|
О.А.
#
15 мая 2009 |
|
|
ABTOPuTET
#
15 мая 2009 |
|
|
О.А.
#
15 мая 2009 |
|
|
ABTOPuTET
#
15 мая 2009 |
|
|
О.А.
#
15 мая 2009 |
|
|
ABTOPuTET
#
15 мая 2009 |
|
|
JlyHATuK
#
16 мая 2009 |
|
|
О.А.
#
16 мая 2009 |
|
|
JlyHaTuK
#
16 мая 2009 |
|
|
О.А.
#
16 мая 2009 |
|
|
Екатерина
#
17 мая 2009 |
|
|
О.А.
#
19 мая 2009 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
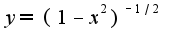 и
используйте известное разложение
и
используйте известное разложение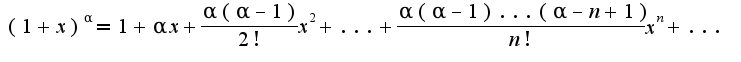
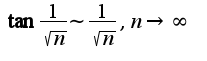
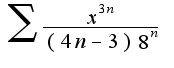 , ( классический вид степенного ряда, к которому применима формула-это наличие степени
, ( классический вид степенного ряда, к которому применима формула-это наличие степени 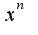 ), поэтому надо воспользоваться признаком Даламбера, найти предел отношения последующего члена ряда к предыдущему и выяснить, когда этот предел меньше единицы
), поэтому надо воспользоваться признаком Даламбера, найти предел отношения последующего члена ряда к предыдущему и выяснить, когда этот предел меньше единицы
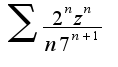
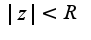 где
где