Форумы
>
Консультация по матанализу
>
объемы тел ограниченных поверхностями, формулы грина, криволинейные интегралы
Поиск
| Автор | Сообщение |
|---|---|
|
Алекс
#
24 мая 2007 |
|
|
О.А.
#
24 мая 2007 |
Форумы
>
Консультация по матанализу
>
объемы тел ограниченных поверхностями, формулы грина, криволинейные интегралы
Чтобы написать сообщение, необходимо войти или зарегистрироваться
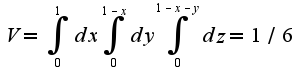 2)Нужно перейти в цилиндрическую систему координат по формулам :
2)Нужно перейти в цилиндрическую систему координат по формулам :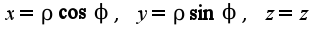 и записать уравнения поверхностей параболоидов в данной системе координат
и записать уравнения поверхностей параболоидов в данной системе координат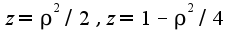 Тогда объем вычисляется по формуле
Тогда объем вычисляется по формуле