Поиск
| Автор | Сообщение |
|---|---|
|
Gerda
#
14 дек 2006 |
|
|
Гоша
#
14 дек 2006 |
|
|
О.А.
#
14 дек 2006 |
|
|
Gerda
#
15 дек 2006 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
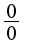 , дифференцируемость функций в числителе и знаменателе в окрестности предельной точки, кроме того, производная от знаменателя не равна нулю)
, дифференцируемость функций в числителе и знаменателе в окрестности предельной точки, кроме того, производная от знаменателя не равна нулю)