Поиск
| Автор | Сообщение |
|---|---|
|
Сергей
#
9 июн 2007 |
|
|
О.А.
#
9 июн 2007 |
|
|
Сергей
#
9 июн 2007 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
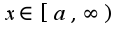 выполняется неравенство
выполняется неравенство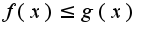 причем интеграл от функции
причем интеграл от функции 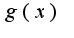 сходится, то будет сходится и исходный интеграл от функции
сходится, то будет сходится и исходный интеграл от функции 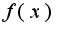 .Для данной функции справедлива оценка
.Для данной функции справедлива оценка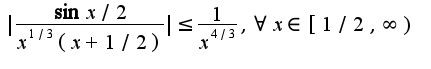 Т.к. интеграл
Т.к. интеграл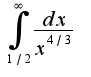 -сходится, то сходится исходный интеграл.
-сходится, то сходится исходный интеграл.