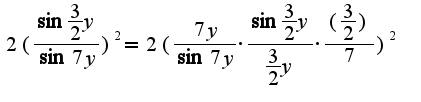Поиск
| Автор | Сообщение |
|---|---|
|
Виталий
#
8 дек 2007 |
|
|
О.А.
#
8 дек 2007 |
|
|
Виталий
#
9 дек 2007 |
|
|
Владимир
#
9 дек 2007 |
|
|
Виталий
#
10 дек 2007 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
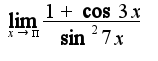 .
При замене
.
При замене 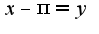 ,
, 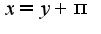 и
и 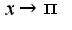 ,
, 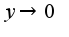 получается
получается 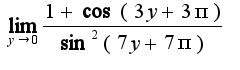 и что с этим дальше делать я не знаю.
Подскажите, пожалуйста.
и что с этим дальше делать я не знаю.
Подскажите, пожалуйста.
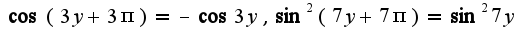 а затем тригонометрическое равенство, связывающее косинус и синус
а затем тригонометрическое равенство, связывающее косинус и синус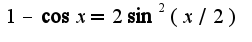 и первый замечательный предел
и первый замечательный предел
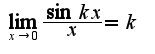 , где
, где 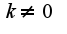 А здесь получается выражение:
А здесь получается выражение:
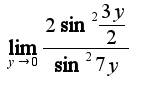 Как же его довести до первого замечательного предела?
Как же его довести до первого замечательного предела?