Поиск
| Автор | Сообщение |
|---|---|
|
Ксюша
#
9 дек 2007 |
|
|
Владимир
#
9 дек 2007 |
|
|
Владимир
#
9 дек 2007 |
|
|
Владимир
#
9 дек 2007 |
|
|
Ксюша
#
9 дек 2007 |
|
|
Владимир
#
9 дек 2007 |
|
|
Владимир
#
9 дек 2007 |
|
|
Ксюша
#
9 дек 2007 |
|
|
Владимир
#
9 дек 2007 |
|
|
Ксюша
#
9 дек 2007 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
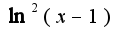 или
или 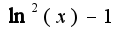
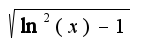 , тк
, тк 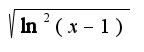 выглядит как то не логично :)
ok
выглядит как то не логично :)
ok
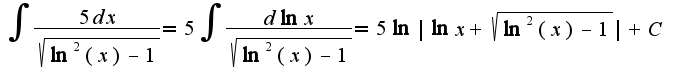
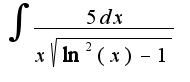
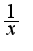 заносим под дифференциал и получаем
заносим под дифференциал и получаем 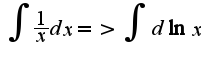 так как
так как 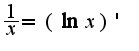 .
Тогда наш интеграл
.
Тогда наш интеграл 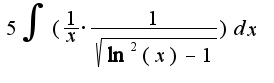 примет вид
примет вид 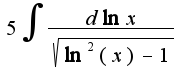 , а это уже табличный интеграл. Если сделать замену
, а это уже табличный интеграл. Если сделать замену 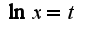 , то получим
, то получим 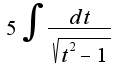 .
Вот :)
.
Вот :)