Поиск
| Автор | Сообщение |
|---|---|
|
Аня
#
19 ноя 2009 |
|
|
О.А.
#
19 ноя 2009 |
|
|
Яна
#
19 ноя 2009 |
|
|
Аня
#
19 ноя 2009 |
|
|
О.А.
#
19 ноя 2009 |
|
|
О.А.
#
19 ноя 2009 |
|
|
Яна
#
19 ноя 2009 |
|
|
Ксения
#
21 ноя 2009 |
|
|
О.А.
#
21 ноя 2009 |
|
|
Ксения
#
24 ноя 2009 |
|
|
Люба
#
3 дек 2009 |
|
|
О.А.
#
3 дек 2009 |
|
|
Люба
#
5 дек 2009 |
|
|
О.А.
#
5 дек 2009 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
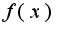 непрерывна в точке
непрерывна в точке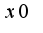 , если
, если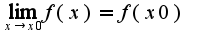 Таким образом, задача сводится к тому, чтобы найти предел в указанной точке, в данном случае в
Таким образом, задача сводится к тому, чтобы найти предел в указанной точке, в данном случае в 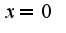 Сл-но, находим предел
Сл-но, находим предел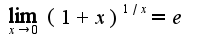 ,
, 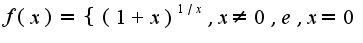 Аналогично решается и второй пример, нужно найти предел функции в точке
Аналогично решается и второй пример, нужно найти предел функции в точке 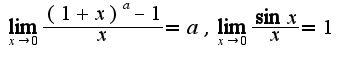 или асимптотические равенства
или асимптотические равенства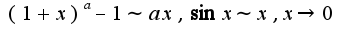 , поэтому
, поэтому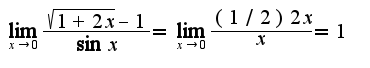 ,сл-но, функция доопределяется в точке
,сл-но, функция доопределяется в точке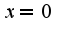 и почему?
и почему?
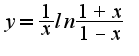
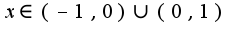 )
http://matan.isu.ru/kons43.jpg
)
http://matan.isu.ru/kons43.jpg