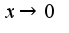Поиск
| Автор | Сообщение |
|---|---|
|
Оля
#
8 янв 2014 |
|
|
o_a
#
8 янв 2014 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
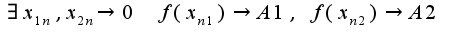 Для данного примера
Для данного примера 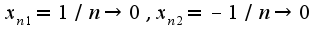 Значения функции на этих последовательноcтях равны
Значения функции на этих последовательноcтях равны 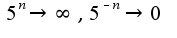 Сл-но, не существует предела
Сл-но, не существует предела 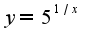 при
при