Поиск
| Автор | Сообщение |
|---|---|
|
Сергей
#
18 дек 2007 |
|
|
Сергей
#
18 дек 2007 |
|
|
О.А.
#
18 дек 2007 |
|
|
Сергей
#
18 дек 2007 |
|
|
Сергей
#
19 дек 2007 |
|
|
Сергей
#
19 дек 2007 |
|
|
Сергей
#
19 дек 2007 |
|
|
О.А.
#
19 дек 2007 |
|
|
Сергей
#
19 дек 2007 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
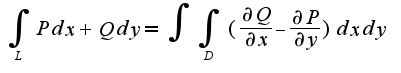 ,где
,где 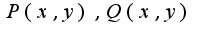 -непрерывны вместе со своими частными производными в области
-непрерывны вместе со своими частными производными в области 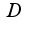 , получим ,что интеграл равен нулю,т.к.
, получим ,что интеграл равен нулю,т.к.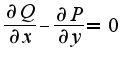 область
область