Страницы: 1 2
Поиск| Автор | Сообщение |
|---|---|
|
Димакова Валя
#
18 апр 2009 |
|
|
О.А.
#
18 апр 2009 |
|
|
Павел
#
19 апр 2009 |
|
|
О.А.
#
19 апр 2009 |
|
|
Павел
#
19 апр 2009 |
|
|
Mordecai
#
20 янв 2013 |
|
|
o_a
#
20 янв 2013 |
|
|
Mordecai
#
20 янв 2013 |
|
|
o_a
#
20 янв 2013 |
|
|
Mordecai
#
20 янв 2013 |
|
|
o_a
#
20 янв 2013 |
|
|
Manana
#
2 мар 2013 |
|
|
o_a
#
2 мар 2013 |
|
|
Manana
#
2 мар 2013 |
|
|
o_a
#
2 мар 2013 |
Страницы: 1 2
Чтобы написать сообщение, необходимо войти или зарегистрироваться
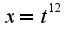
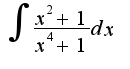 Заранее Спасибо!
Заранее Спасибо!
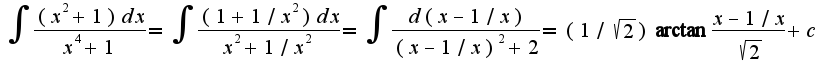
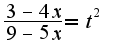
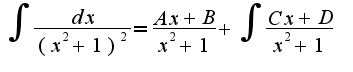 , находят неопределенные коэффициенты, приравнивая коэффициенты слева и справа в равенстве при одинаковых степенях
, находят неопределенные коэффициенты, приравнивая коэффициенты слева и справа в равенстве при одинаковых степенях  . Получим
. Получим 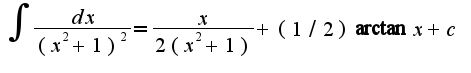
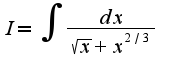 , то нужно сделать замену
, то нужно сделать замену 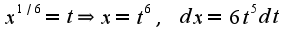 ,чтобы избавиться от корней, (выбирая общий знаменатель дробей
,чтобы избавиться от корней, (выбирая общий знаменатель дробей 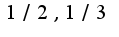 ), затем пересчитать подинтегральное выражение в новой переменной
), затем пересчитать подинтегральное выражение в новой переменной 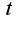 .Получим
.Получим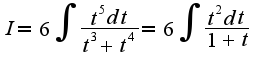 Под знаком интеграла получилось рациональное выражение, дробь неправильная, т.к. в числителе показатель выше, чем в знаменателе, поэтому выделяем целую часть, делим
Под знаком интеграла получилось рациональное выражение, дробь неправильная, т.к. в числителе показатель выше, чем в знаменателе, поэтому выделяем целую часть, делим 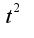 на
на 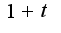 , получим
, получим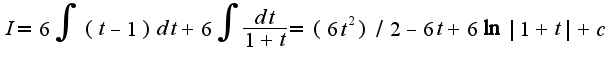 Возвращаясь к исходной переменной, получим
Возвращаясь к исходной переменной, получим 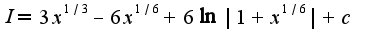
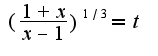 . В целом, решение повторяет логику рассуждений при решении предыдущего примера.
. В целом, решение повторяет логику рассуждений при решении предыдущего примера.