Поиск
| Автор | Сообщение |
|---|---|
|
Жанна
#
13 янв 2008 |
|
|
О.А.
#
13 янв 2008 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
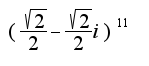
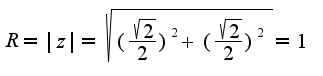
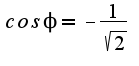
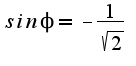
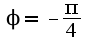
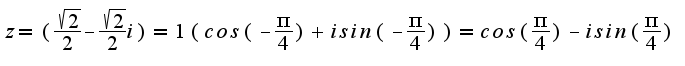
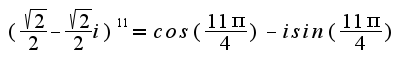 Спасибо Вам огромное за ту помощь, которую Вы нам оказываете!
Спасибо Вам огромное за ту помощь, которую Вы нам оказываете!
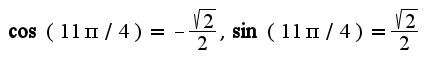 и еще
и еще