Поиск
| Автор | Сообщение |
|---|---|
|
paniker
#
19 янв 2009 |
|
|
О.А.
#
19 янв 2009 |
|
|
paniker
#
19 янв 2009 |
|
|
О.А.
#
19 янв 2009 |
|
|
paniker
#
19 янв 2009 |
|
|
О.А.
#
19 янв 2009 |
|
|
paniker
#
21 янв 2009 |
|
|
О.А.
#
21 янв 2009 |
|
|
paniker
#
22 янв 2009 |
|
|
О.А.
#
22 янв 2009 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
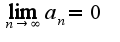 , для данного ряда он не выполняется,т.к.
, для данного ряда он не выполняется,т.к.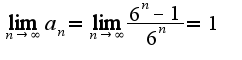
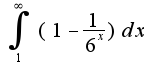
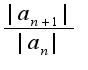 , т.к. это соотношение больше 1, то ряд расходится
, т.к. это соотношение больше 1, то ряд расходится