Поиск
Алексей
#
27 ноя 2006
|
Уважаемая Ольга Александровна.
У меня из дз не получается...Помогите пожалуйста.
1. f(x)=(ln(x))/(1-x)^2 , g(x)=1/(1-cos((x-1)^(1/2))), x->1+
a)показать, что данные функции f и g являются бесконечно малыми или бесконечно большими при указанном стремлении аргумента
б)для каждой функции f и g записать главную часть вида С(х-х0)^alfa при х->x0 или Сх^alfa при x->беск, указать их порядки малости(роста)
в)Сравнить f и g
2.Найти точки разрыва функции f(x) и определить их характер, Дать графическую иллюстрацию.
f(x)={cos(pi*x/2), при |x|>1 и (tg(pi*x))/arcsin(x), при |x|<=1
И еще хотел спросить, я вот эти темы пропустил, подскажите, где можно найти методички, или др учебные пособия, чтобы нагнать упущенное.
Спасибо.
|
О.А.
#
27 ноя 2006
|
Данные темы подробно представлены в любом учебнике по математическому анализу
1) Ильин В.А., Садовничий В.А., Сендов Б.Х. Математический анализ. Т.1,2. Из-во МГУ, 1985.
2) Кудрявцев Л.Д. Математический анализ. Т.1,2. М.:Высшая школа, 1973.
3) Ильин В.А., Позняк Э.Г. Основы математического анализа.Т.1,2.М.:Наука, 1982.
4)Зорич В.А.Математический анализ.Т.1,2.М.:Наука,1984.
5)Демидович Б.П.Сборник задач и упражнений по курсу математического анализа.М.:Наука,1972.
6) Ляшко И.И., Боярчук А.К.Справочное пособие по математическому анализу. Киев:Вища школа,1984.
7) Кудрявцев Л.Д. и др. Сборник задач по математическому анализу. Спб.,1994.
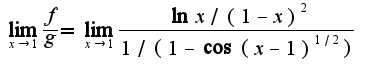 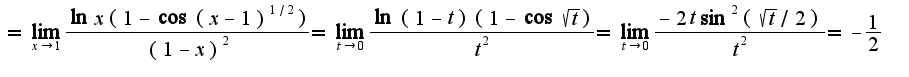 Поэтому данные функции являются функциями одного порядка при 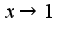
|
Ваш ответ:
|
|
Чтобы написать сообщение, необходимо войти или зарегистрироваться
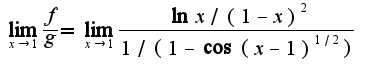
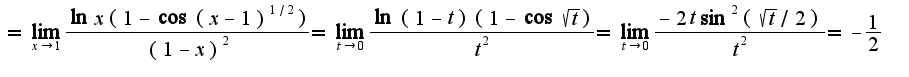 Поэтому данные функции являются функциями одного порядка при
Поэтому данные функции являются функциями одного порядка при