Поиск
| Автор | Сообщение |
|---|---|
|
elochka
#
10 фев 2011 |
|
|
o_a
#
10 фев 2011 |
|
|
elochka
#
12 фев 2011 |
|
|
paulinio
#
22 ноя 2011 |
|
|
o_a
#
22 ноя 2011 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
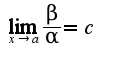 (предел конечен и не равен 0), то α и β являются бесконечно малыми величинами одного порядка малости.в данном примере
(предел конечен и не равен 0), то α и β являются бесконечно малыми величинами одного порядка малости.в данном примере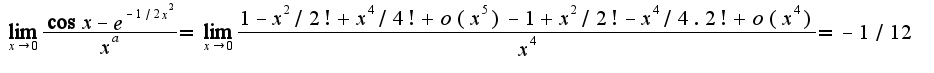 для нахождения предела использована формула Маклорена для функций косинус и экспоненты. Следовательно, порядок указанной функции равен 4
для нахождения предела использована формула Маклорена для функций косинус и экспоненты. Следовательно, порядок указанной функции равен 4
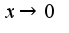 функции, т.е.
функции, т.е. 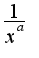 число
число 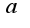 и будет указывать порядок
и будет указывать порядок