Поиск
| Автор | Сообщение |
|---|---|
|
Настя
#
1 ноя 2008 |
|
|
О.А.
#
1 ноя 2008 |
|
|
Настя
#
2 ноя 2008 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
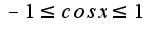 то
то
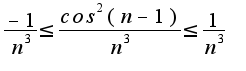 т.е. можно просто написать
т.е. можно просто написать 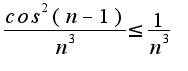 и правильно ли писать, что
и правильно ли писать, что 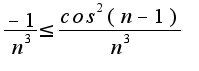 , а именно (-1), ведь там cos в квадрате
, а именно (-1), ведь там cos в квадрате
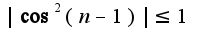 , кроме того, рекомендую график построить данных функций и сравнить
, кроме того, рекомендую график построить данных функций и сравнить