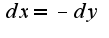Поиск
| Автор | Сообщение |
|---|---|
|
Vitaliy
#
23 дек 2009 |
|
|
О.А.
#
23 дек 2009 |
|
|
Vitaliy
#
24 дек 2009 |
|
|
О.А.
#
24 дек 2009 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
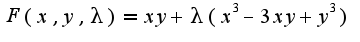 Далее составляю систему уравнений, состоящую из:
Далее составляю систему уравнений, состоящую из:
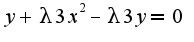
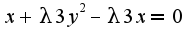
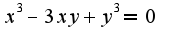 А дальше не могу разобраться, как лучше решить данную систему, и вообще составлена ли она верно? и какие действия принимать после решения тоже не совсем понятно..
Надеюсь на помощь.
Виталий.
А дальше не могу разобраться, как лучше решить данную систему, и вообще составлена ли она верно? и какие действия принимать после решения тоже не совсем понятно..
Надеюсь на помощь.
Виталий.
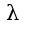 из первого и второго уравнений, затем приравнять и найти зависимость между
из первого и второго уравнений, затем приравнять и найти зависимость между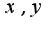 , ответ
, ответ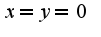 ,
,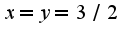 Для определения какого вида экстремум составляют дифференциал второго порядка от функции Лагранжа и определяют его знак
Для определения какого вида экстремум составляют дифференциал второго порядка от функции Лагранжа и определяют его знак
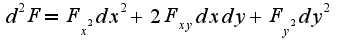 , кроме того из уравнения связи следует, что
, кроме того из уравнения связи следует, что