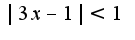| Автор | Сообщение |
|---|---|
|
Юлия
#
29 мая 2009 |
|
|
О.А.
#
30 мая 2009 |
|
|
Mike
#
30 мая 2009 |
|
|
О.А.
#
30 мая 2009 |
|
|
Mike
#
31 мая 2009 |
|
|
О.А.
#
31 мая 2009 |
|
|
Mike
#
1 июн 2009 |
|
|
О.А.
#
1 июн 2009 |
|
|
Mike
#
1 июн 2009 |
|
|
О.А.
#
2 июн 2009 |
|
|
Mike
#
2 июн 2009 |
|
|
Mike
#
2 июн 2009 |
|
|
О.А.
#
2 июн 2009 |
|
|
Люба
#
3 июн 2009 |
|
|
О.А.
#
3 июн 2009 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
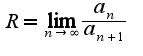 , где
, где 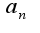 -коэффициент ряда, область (интервал)сходимости
-коэффициент ряда, область (интервал)сходимости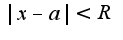 затем проверяется сходимость на концах интервала сходимости
затем проверяется сходимость на концах интервала сходимости
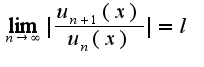 если
если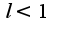 , то ряд сходится
2) используйте признак сравнения, получите мажоранту для данного ряда
, то ряд сходится
2) используйте признак сравнения, получите мажоранту для данного ряда