Поиск
Демидович
#
8 янв 2007
|
Здравствуйте! С прошедшим, Вас, Новым годом и Рождеством!
Вот не могу никак решить 3 примера из Демидовича...
586) Lim( (Ln(1+x)/(1-x))/arctg(1+x)-arctg(1-x) )
655) Пусть х->1. Выделить главный член вида C(х-1)^n и определить порядки малости относительно беск. малой х-1 след. ф-и:
б) (1-(х)^1/2)^1/3
г) е^x-e
656)Пусть х->+oo. Выделить главный член вида Cх^n и определить порядки роста относительно беск. большой х след. ф-и:
в) (x^2-x)^1/2+x^1/2
Буду очень признателен за помощь...
|
О.А.
#
8 янв 2007
|
Вас тоже с Новым годом и Рождеством!
1)Известна формула: 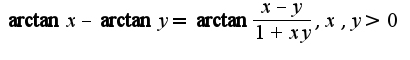 Поэтому 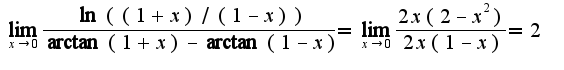
2) Чтобы найти главную часть, надо сделать замену переменной 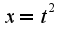 , тогда 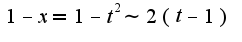 при этом 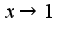 сл-но, 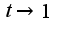 Тогда функция примет вид:  Это и есть главная часть данной функции при 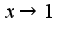 . Остальные примеры решаются аналогично. Удачи!
|
Ваш ответ:
|
|
Чтобы написать сообщение, необходимо войти или зарегистрироваться
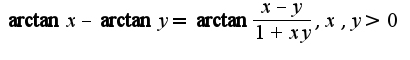 Поэтому
Поэтому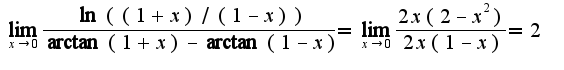 2) Чтобы найти главную часть, надо сделать замену переменной
2) Чтобы найти главную часть, надо сделать замену переменной 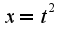 , тогда
, тогда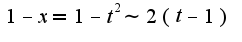 при этом
при этом 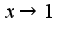 сл-но,
сл-но, 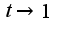 Тогда функция примет вид:
Тогда функция примет вид: Это и есть главная часть данной функции при
Это и есть главная часть данной функции при